Útmutató az 1. laborhoz

Laborfeladatok:

A laborfoglalkozás végén töltse fel az elkészített fuggvenyeim.cpp és fuggvenyeim.h fájlokat valamint az f1.txt jegyzőkönyvet a Jporta rendszerbe (1. önellenőrző feladat), hogy megkapja a labor elvégzéséért járó pontot! A laborgyakorlatokon elvégzett feladatok feltöltésére a minden esetben laborgyakorlatot követő szombat 06:00-ig van lehetősége.

Eszközök

A laborfeladatok megoldásához tetszőleges fejlesztőkörnyezetet használhat. A HSzK laborjaiban a CodeBlocks, VSCode, ill. a VisualC++ érhető el, de számos más eszköz is létezik a C++ programok fejlesztéséhez, amelyeket saját gépén, vagy a kari felhőben kialakított gépen ki is próbálhat/használhat.

A fordítás lépései 30-40p

A következő feladatokhoz készítsen egy szöveges (f1.txt), rövid jegyzőkönyvet. A jegyzőkönyvben írja le, hogy mit tapasztalt, milyen kimenet jelent meg a képernyőn, az megegyezett-e a várt kimenettel. A jegyzőkönyv első sorába írja bele a NEPTUN kódját!

Indítsa el a MSYS2 UCRT64 környezetet, az MSYS2-ről bővebben itt olvashat. Keresse meg a home könyvtárát a számítógépgép meghajtóján! (A pwd parancs hasznos, keresse a C meghajtó/msys64 könyvtárban)
Készítsen egy egyszerű c++ programot (main.cpp) a következő tartalommal. Tetszőleges szerkesztő használható, pl. emacs vagy vim a konzolban, illetve az egyszerűen Notepad++-t használhatjuk a windows felől is. (a korábban megtalált helyre elnavigálva) Ugyanakkor a fordításhoz tartozó parancsokat már az MSYS2 UCRT64 konzolban adjuk ki! A vim szerkesztőhöz összefoglaló: VIM, alapok - kezdőknek .
Például: nvim main.cpp majd i (szerkesztői mód), a kód, nyilakkal navigálás, szerkesztés, majd ESC és végül elmentjük és kilépünk: :wq A konzolba való beillesztéshez használja a jobb egérgomb, beillesztés funkciót!
```
#include <iostream>
int main() {
        std::cout << "Hello" << std::endl;
        return 0;
}
```
A futtatható állomány előállításához a háttérben a következő lépések hajtódnak végre: előfeldolgozás (preprocesszálás), fordítás majd linkelés. Ezt a g++ és clang++ esetén külön-külön lépésekben végre tudjuk hajtani. Nézzük meg a g++ --help parancs kimenetét! Milyen opciókat tudunk beállítani a kapcsolókkal?
Adjuk ki a g++ -E main.cpp parancsot. Láthatjuk, hogy az include le lett cserélve az iostream-hez tartozó tartalomra. A preprocesszort semmilyen módon nem érdekli a C/C++ szintaktikája és szemantikája, egyszerű szövegfeldolgozást végez.
Feladat: Van egy állományunk nagyon sok "ALMA", "SZILVA", "KORTE" szavakkal. Cseréljük le ezeket számokra a preprocesszort használva! Segítség: nevezzük át az állományt .cpp (pl. gy.cpp) kiterjesztésűre, és használjuk a #define makrót! Próbáljuk ki a következő fájlon:
```
#define ALMA 0
#define KORTE 1
#define SZILVA 2
ALMA,KORTE,KORTE,SZILVA,ALMA,ALMA ...
```
A következő fázis a fordítás: Ekkor a forrásfájlokból az előfeldolgozást követően object állomány (.o/.obj) készül. Ezek a fájlok ugyan gépi utasításokat tartalmaznak, de közvetlenül nem futtathatóak. Hozzuk létre a következő állományokat, majd fordítsuk le őket a g++ -c main2.cpp és g++ -c foo.cpp parancsokkal (két .o kiterjesztésű fájlt kapunk, ls parancs).
```
// main2.cpp:
void foo(const char*);
int main() {
        foo("Hello");
        return 0;
}
// foo.cpp:
#include <iostream>
void foo(const char* str) {
        std::cout << str << std::endl;
}
```
A két object fájl összeállításához adjuk ki a következő parancsot: g++ main2.o foo.o -o main2. Végül futassuk a programot: ./main2. Mivel azonos névkonvenciók szerepeltek, a linkelés megtalálta a foo függvény definícióját a másik állományban. Mivel a deklarációkat nehéz karbantartani, ha nagyon sok helyen használunk egy-egy függvényt, ezért szokás azt egy fejlécfájlba kiszervezni és utána azt include-olni. (Ahogy korábban is tanultuk)
Egy függvényt akárhányszor deklarálhatunk, viszont csak egyszer definiálhatunk (One Definition Rule). Ez akkor okozhat problémát, ha egy header fájlban definíció is szerepel, ekkor az include-ok miatt előfordulhat, hogy több definíció is előáll egy-egy függvényből. Ezt elkerülendő, makrókat használunk a "felesleges" definíciók kiszűrésére: Ezt szokás include guard-nak hívni. Ezek az őrök eldobják a fejlécfájl tartalmát, ha már feldolgozásra került. Példa:
```
// main3.cpp
#include "bar.h"
#include "bar.h" // jöhet egy másik include-ból is
int main() {
        return 0;
}
// bar.h
#ifndef BAR_H //include guard
#define BAR_H

void bar() { }

#endif
```
Nézzük meg mi lesz a preprocesszor kimenete: g++ -E main3.cpp Ez miért jó nekünk? Próbáljuk ki úgy is, ha kitöröljük az include guard-ot!
Érdemes bekapcsolni a figyelmeztetéseket a fordításkor, ezt a -Wall kapcsolóval tudjuk megadni, ami több lehetséges hibaforrás azonosításában is segítségünkre lehet. Készítsünk egy új forrásfájlt warnings.cpp néven, a lenti tartalommal, mi az ami problémát okozhat? Ha megvan a válasz, fordítsuk le a következő paranccsal: g++ -Wall -o warnings warnings.cpp Ezt a figyelmeztető üzenetet vártuk?
```
#include <iostream>
int main() {
        int a;
        std::cout << a << std::endl;
        std::cout << "Hello" << std::endl;
        return 0;
}
```
Milyen funkciókat nyújtanak a -g, -Werror és -O0 kapcsolók? Nézzen utánna! Hasznos oldal ehhez: g++ file -g -Wall -Werror -O0
Készítse el a lenti C++ kódot! A nyelv folyamatosan fejlődik, új standardokkal, verziókkal bővül. Fontos, hogy ezek a verziók visszafele kompatibilisek legyenek.
```
//auto.cpp
#include <iostream>
int main() {
        auto i = 10 + 2;
        std::cout << i << std::endl;
        return 0;
}    
```
A verziókat az -std=[verzió] kapcsolóval állíthatjuk, ha a használt fordító támogatja a kiválasztott standardot. Próbáljuk ki a fenti kódon a következő standardokat:
- g++ -std=c++98 -o auto auto.cpp
- g++ -std=c++03 -o auto auto.cpp
- g++ -std=c++11 -o auto auto.cpp
- g++ -std=c++14 -o auto auto.cpp
Mikor, melyik verzióban jelent meg valószínűleg ez az 'auto' kulcsszó?

A labor végén kérem adja le az elkészített szöveges jegyzőkönyvet (f1.txt) a "JPORTA feladat"tal (következő rész) együtt a JPORTA oldalon! A jegyzőkönyvbe írja bele a NEPTUN kódját is!

JPORTA Feladat

Jelentkezzen be a Jporta rendszerbe az egyetemi eduID azonosítójával, és oldja meg az első kötelező feladatot (Neptun kód)! Az első héten ez az apró feladat megoldása helyettesíti a laborgyakorlatra felkészítő ellenőrző feladatot. A továbbiakban a laborgyakorlatokra felkészítő feladatokat mindig a laborgyakorlat hetén kedd reggel 6 óráig kell megoldani.

A Git verziókezelő rendszerről egy rövid összefoglaló itt található.

Programoknak, dokumentumoknak rendszerint több változatát tároljuk. A változatok közötti eligazodást, a változatok kezelését ún. verziókövető (verziókezelő) rendszerek segítik. Ezek lényege, hogy tárolóban (repository) együtt tárolnak több változatot melyek közül kiválaszthatjuk, hogy melyikkel szeretnénk dolgozni. Ehhez a tárgyhoz kapcsolódó anyagokat, forrásprogramokat is egy ilyen verziókezelő rendszerben kezeljük, melynek a neve Git. Ebben a rendszerben az összetartozó fájlokat, könyvtárakat ún. projektekbe kell szervezni. A tárolt dokumentumok, forráskódok egy egyszerű böngészővel is elérhetők, de speciális klienssel könnyebb az anyagok elérése. A HSZK-ban telepített TortoiseGit kliens beépül a Windows fájlkezelőjébe. Segítségével könnyű egy teljes projekteket letölteni a tárolóból. Ebben a félévben a laborok nagy részénél előkészített fájlokon kell dolgozni, melyek a tantárgy Git tárolójából tölthetők le. Minden laboranyagot külön projektbe, a projekteket pedig a labor_peldak nevű csoportba szerveztük.
Kérje le az első laborhoz előkészített fájlokat a tantárgy Git tárolójából, melynek elérési útvonala:
https://git.ik.bme.hu/Prog2/labor_peldak/lab_01.git!
1. Másolja ki vágólapra a feladat URL-jét! Ezt a Gitlab webes felületén is elvégezheti.
2. A Hozzon létre a munkához egy üres katalógust!
3. A létrehozott (pl. labor) katalóguson jobb egérgombbal kattintva a feljövő menüből válassza ki a Git Klónozás...(Git Clone...) menüpontot, majd a feljövő panelen a tároló (Repository) elérési útjaként (URL) állítsa be a vágólapra másolt URL-t, majd indítsa el a letöltést (OK gomb)!
  Az URL-t a TortoiseGit kliens a vágólapról automatikusan bemásolja, így azt csak el kell fogadnia.
  A kliens nyelvi beállítását a TortoiseGit menupont Beállítások (Settings) almenüjében lehet változtatni.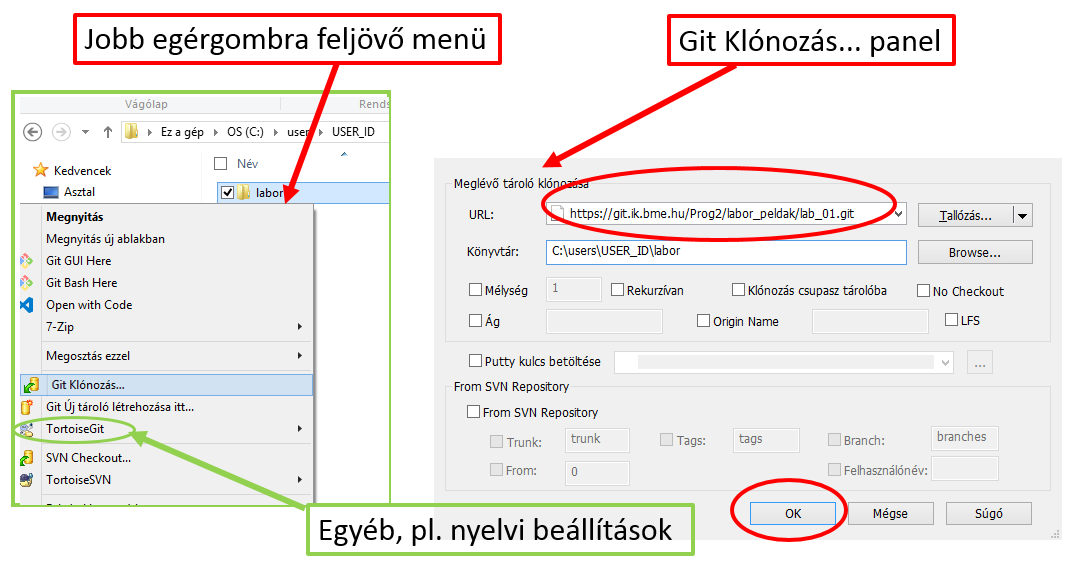
4. A fájlkezelővel nézze meg, hogy mi töltődött le a kijelölt katalógusba. Sikeres letöltés esetén egy szövegfájlt (README.TXT) és egy alkatalógust (nagyobb) kell látnia.

Ha más fejlesztőkörnyezetet preferál, akkor abban hozzon létre egy új C++ console projektet, és adja hozza a nagyobb katalógusban levő *.cpp és *.h fájlokat!

Lépjen be a nagyobb alkatalógusba! Ebben az előadáson bemutatott egyszerű program fájljait találja, valamint a programokhoz tartozó CodeBlocks projektfájlt, illetve egy Makefile-t egyéb könyezetekhez pl. Linux/MacOS, Clion, stb. Ha projektfájlra kattintva nem indul a CodeBlocks, indítsa azt el, majd húzza rá a megnyíló ablak fejlécére a projektfájlt!
Röviden tekintse át a kódot, fordítson és futtasson!
Tervezzen egy olyan függvényt (először csak a deklarációját/prototípusát kell megadnia), ami kiszámolja egy n-ed fokú valós polinom helyettesítési értékét. A függvény paraméterként kapja egy valós tömbben a polinom együtthatóit (0. fokú a 0. indexű helyen). Szintén paraméterként kapja a polinom fokszámát és a független változót.
Laborvezetőjével beszélje meg a függvény paramétereit és azok típusát (pointer? konstans? referencia?) és írja be a függvény prototípusát (deklarációját) a fuggvenyeim.h fájlba.
???
Tömb paraméterként történő átadása C++-ban is a tömb első elemének címével történik. Mivel az együtthatókat tartalmazó tömböt a függvény nem fogja módosítani, célszerű konstans tömbként átadni pl. így:
```
/**
 * polinom helyettesítési értéke
 * @param x - független változó
 * @param double const *a - együtthatók tömbje (a[0] a 0. együttható)
 * @param n - polinom fokszáma
 */
double polinom(double x, double const *a, int n);
```
vagy így:
```
double polinom(double x, double const a[], int n);
```

Tegye alkalmassá a főprogramot (nagyobb_main) a függvény kipróbálásához! pl:

...
    double an[] = { 3, 2, 1 }; // együtthatók: a0=3, a1=2, a2=1      
    cout << "polinom(x=1)(x^2+2x+3):" << polinom(1.0, an, 2) << endl;
...

a3*x^3 + a2*x^2 + a1*x + a0 = ((a3*x+a2)*x+a1)*x+a0

Készítse el (definiálja) a függvényt a fuggvenyeim.cpp fájlban! Az n. hatvány kiszámolása helyett alakítsa a polinomot szorzattá! (Horner elrendezés)

???

/**
 * polinom helyettesítési értéke
 * @param x - független változó
 * @param double const *a - együtthatók tömbje (a[0] a 0. együttható)
 * @param n - polinom fokszáma
 */
double polinom(double x, double const *a, int n) {
    double y = 0;
    for (int i = n ; i >= 0; i--) {
        y = y * x + a[i];
    }
    return y;
}

Próbálja ki a függvényt: fordítson, futtasson, majd cserélje le a főprogramot az alábbi kezdetleges tesztprogrammal!

...
int main() {
    double an[] = { 3, 2, 1 }; // együtthatók: a0=3, a1=2, a3=1      
    double res[] = { 3, 6, 11, 18, 27, 38, 51 };
    int hibak = 0;
    for (int i = 0; i < 7; i++) {
        double x = i;
        double fx = polinom(x, an, 2);
        if (res[i] != fx) {    // Helyes ez így? 
           cout << "Hibas: " << res[i] << "!=" << fx << endl;
           hibak++;
        }
    }
    if (hibak == 0)
        cout << "Nem volt elteres" << endl;
}

Ha hibátlanul fut a fenti teszt, akkor biztosak lehetünk a függvényük helyességében? Beszélje ezt meg a laborvezetőjével!

Cserélje le a for cilusban a double x = i; utasítást az alábbi utasításokkal, majd fordítson, futtasson!
```
        const double Z = 3.141e2;
        double x = i / Z - 1;
        x++;
        x = x * Z;
```
Mit tapasztal?

A manipulátorokról a 2. előadáson lesz részletesebben szó.

Módosítsa a kódot, hogy 20 tizedesjegyre írja ki az értékeket! Ezt a setprecision manipulátorral a legegyszerűbb elérni:
```
...
           cout << "Hibas: " << setprecision(20) << res[i] << "!=" << fx << endl;
...
```
A módosított kód futtatásával egyértelművé válik, hogy a valós számokkal végzett műveletek eredménye a számábrázolásból fakadó pontatlanságok miatt nem pontos. Ezért az eredmények összehasonlításakor óvatosan kell eljárni.

Módisítsa a főprogramot úgy, hogy az almostEQ függvényt használja összehasonlításra (ld. függvényeim.h)!.

???

/// Végleges főorgram
int main() {
    double an[] = { 3, 2, 1 }; // együtthatók: a0=3, a1=2, a3=1
    double res[] = { 3, 6, 11, 18, 27, 38, 51 };
    int hibak = 0;
    for (int i = 0; i < 7; i++) {
        const double Z = 3.141e2;
        double x = i / Z - 1;
        x++;
        x = x * Z;
        double fx = polinom(x, an, 2);
        // almostEQ: A legkisebb érték 50-szereséhez hasonlítja a relatív és abszolút hibát 
        if (!almostEQ(res[i], fx)) {    
           cout << "Hibas: " << setprecision(20) << res[i] << "!=" << fx << endl;
           hibak++;
        }
    }
    if (hibak == 0)
        cout << "Nem volt elteres" << endl;

}

Ne felejtse el feltölteni elkészített fuggvenyeim.cpp és fuggvenyeim.h fájlokat a Jporta rendszerbe (polinom, 1. önellenőrző feladat)! A feltöltött fájlokat a Jporta csak lefordítja. A megoldás helyességét a laborvezető ellenőrzi.

Ha még maradt idő:
Fakultatív feladatok:

Indítson egy virtuális gépet a kari felhőben linux operációs rendszerrel! Ehhez egy később megoldandó fakultatív feladat leírásában talál segítséget (Virtuális gép indítása az IK-IIT felhőben című feladat első 5 lépése). Parancsokhoz segítség: unix alapok
Lépjen be a gépre, majd hajtsa végre a következő parancsokat:

Most nézzünk egy másik feladatot:

git clone https://git.ik.bme.hu/Prog2/labor_peldak/lab_01.git # a lab_01 katalógusba másolódik az első labor anyaga
cd lab_01/nagyobb                # belépünk a lab_01 könyvtárba
ls -l                            # kilistázzuk annak tartalmát

Fordítsa le az előadás példáját a g++ nagyobb_main.cpp fuggvenyeim.cpp -o nagyobb paranccsal!, majd
Futtassa a programot a ./nagyobb paranccsal! Az input végén nem CTRL-Z, hanem CTRL-D kell!

Próbálja ki a make parancsot is:

make                             # Ha ez előző fordítás sikeres volt, nem csinál semmit 
make clean                       # a clean szabályt hajtja végre, ami törli a eredményfájlokat 
ls -l 
make                             # most újból előállítja az a programot
ls -l

Próbálja ki a gdb debuggert! Ez egy parancssoros egyszerű program, ami alfanumerikus környezetben is működik: gdb -tui nagyobb A parancs elindítja a debuggert. A megnyíló kvázi grafikus ablakban láthatóvá válik a forráskód. Alatta pedig a gdb parancsra vár. A teljesség igénye nélkül az alábbiakban áttekintünk néhány gdb parancsot, melyeket bátran próbáljon ki!
- b 9 - a 9. sorba tesz egy töréspontot
- r - elindítja a programot, ami meg fog állni a 9. sornál
- s - végrehajtja az aktuális C utasítást
- s - ismét végrehajt, de mivel input utasítás következik, várni fog a két egész számra, amit echon nélkül, vakon kell begépelnie (pl: 4 5 ENTER).
- p i - kiírja az i változó értékét
- q - kilép a programból
Önálló munkához a következő feladatokat ajánlom: feladat1.html

A védelmi rendszer mélyebb gyakorlati áttekintéséhez egy olyan számítógépre van szükség, ahol két különböző felhasználónévvel is rendelkezik, vagy van egy másik kolléga, akinek szintén van hozzáférése a géphez. Ilyen központi gép jelenleg nincs HSzK-ban. Ha van VIK felhőben gépe, akkor abban (Gyakorló feladat a védelmi rendszer bemutatásához.)

Jó munkát!

Utolsó frissítés: 2024-02-17 18.30

Keresés űrlap

Útmutató az 1. laborhoz

Laborfeladatok:

Eszközök

A fordítás lépései 30-40p

JPORTA Feladat

Főmenü